Direct sampling methods for nonlinear inverse problems.
Contributor: Malcolm Sambridge, RSES Australian National University, Malcolm.Sambridge@anu.edu.au.
Project Description
Because geophysical observations are made at (or very near) the Earth’s surface, all knowledge of the Earth’s interior is based on indirect inference. The aim of our research is to develop new classes of mathematical and computational approaches to large-scale nonlinear inversion with application to geophysical problems, e.g., seismic tomography. The emphasis is to move away from mere parameter estimation to a characterisation of appropriate models. A particular focus is on Bayesian sampling methods applied to cases where both the number of unknowns to be solved for as well as the level of noise in the data are not know a priori. We develop and apply new transdimensional sampling methods which use the variability of the data to decide on the complexity of the model as well as the noise in the data.
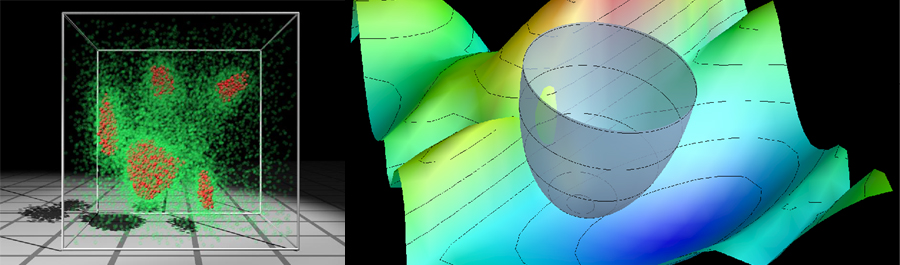
The first figure shows an example of nonuniqueness in the inversion of airborne Electromagnetic data for subsurface conductivity structure. The lower left panel shows an ensemble of three layer depth-conductivity profiles that all produce airborne signals that fit observations equally well (upper panels). The lower right panel shows profiles with similar levels of data fit using 15 layers for the subsurface. How does one select between such alternate representations in an objective manner? Transdimensional Bayesian sampling methods we are developing allow inversions to be performed which jump between different styles of model representation in a consistent fashion. The result is an ensemble of solutions, rather than a single optimal model, that characterize the complete solution space.
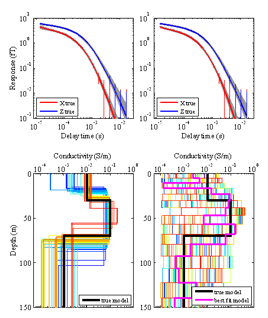
Figure 1. An illustration of non-uniqueness in the inversion of AEM data.
The second figure shows an example of a data misfit landscape as a function of two unknowns in a toy inverse problem in seismic imaging. As more data are introduced (panels a, b, c) the peak of data misfit function becomes better defined but the misfit landscape also becomes more complex making the problem more difficult to solve. A multi-scale staged approach is suggested where simpler problems are solved first and more complexity is gradually introduced. We are developing new inversion algorithms based on these principles.
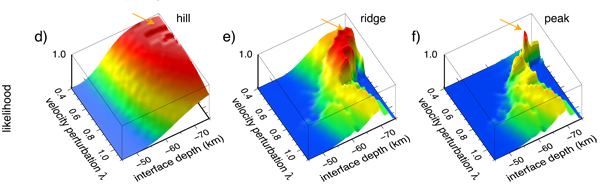
Figure 2. Hill Plateau Peak.
Direct search/global optimization methods that we use, develop and modify include The Neighbourhood Algorithm, Simulated Annealing, Genetic Evolutionary Algorithms as well as grid search. We have an ongoing program research theme in development of new direct search techniques. A goal is to extend the range of the problems to which they can be applied (in terms of the number of unknowns) and also their use in addressing issues of uncertainty of inversion results.
Collaborators: Thomas Bodin (ANU), Kerry Gallagher (Univ. of Rennes, France), Brian Kennett (ANU).
More about this Project
Neighbourhood algorithm – http://www.iearth.edu.au/codes/NA/ (opens in a new tab/window)
Publications
Seismic tomography with the reversible jump algorithm,
Bodin, T., and Sambridge, M., Geophys. J. Int., 178, 1411-1436, doi:10.1111/j.1365-246X.2009.04226.x, 24th April 2009.
A self-parameterising partition model approach to tomographic inverse problems,
Bodin, T., Sambridge, M., and Gallagher, K., Inverse Problems, 25, 055009, doi:10.1088/0266-5611/25/5/055009, 17th March 2009.
Markov chain Monte Carlo (MCMC) sampling methods to determine optimal models, model resolution and model choice for Earth Science problems,
Gallagher, K., Charvin, Nielsen, S., Sambridge, M., and Stephenson, J., Marine and Petrol. Geol., 26, 525-535, doi:10.1016/j.marpetgeo.2009.01.003, 15th January 2009.